We revisit the teleportation of two qubits entanglement using a single channel made of a single Majorana wire connecting two pairs of qubits each at the sending and receiving ends of the wire. The scheme is different from that use in our early work (Phys. Scr. 95 035803 (2020)) where the two qubit teleportation required two copies of the Majorana wires setup as required to implement the Lee and Kim teleportation scheme. The two pairs of qubit interact via the exchange coupling. It is in this setting that we investigate the role of the exchange coupling, the channel parameters, the spin chain parameters on the average fidelity of entanglement teleportation. We equally consider the fact that the geographically located two pairs of qubits interact differently with their respective spin chain environment. The dynamics of the average fidelity is shown to be enhanced when using a set-up with symmetric coupling between qubits and Majorana wire at both ends as compared to when using asymmetric coupling. Small values of the coupling between the qubits and spin environments should however be used. Large values of the exchange coupling between qubits in the two sub-systems should be used to have high fidelity of the teleported state. The dynamics of the average fidelity of entanglement teleportation is seen to depend on the size of the spin environment as compared to the teleportation protocol used in our earlier work where the dynamics is mildly sensitive to the size of the spin environment. Increasing the strength of the transverse magnetic field and large values of the anisotropy degree enhances the average fidelity of entanglement teleportation. The same observation is seen when considering the same values of the coupling between the two qubits sub-systems at the opposite ends of the Majorana wire and their respective spin environment. The dynamics of the system is however seen to observe almost a similar trend as that of the above cited work for the single Majorana wire setup.
| Published in | American Journal of Modern Physics (Volume 14, Issue 5) |
| DOI | 10.11648/j.ajmp.20251405.12 |
| Page(s) | 222-233 |
| Creative Commons |
This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited. |
| Copyright |
Copyright © The Author(s), 2025. Published by Science Publishing Group |
Spin Chain Environment, Qubits, Single Majorana Wire, Entanglement Teleportation, Average Fidelity
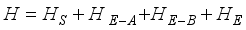 (1)
(1) 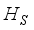 describes the MBSs plus the single-level two pairs of QDs and their mutual coupling as follows
describes the MBSs plus the single-level two pairs of QDs and their mutual coupling as follows 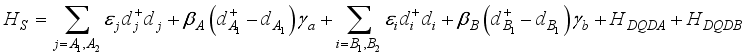 (2)
(2) 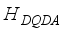 and
and 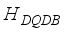 in equation (2) are the Hamiltonians for the interactions between the QDs of sub-system A and B respectively and are given as
in equation (2) are the Hamiltonians for the interactions between the QDs of sub-system A and B respectively and are given as 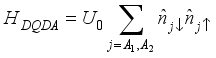 and
and 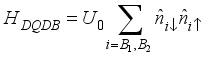 .
. 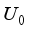 is Coulomb interaction strength
is Coulomb interaction strength 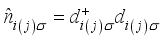 and
and 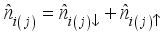 where
where 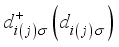 are annihilation (creation) operators of the single level QDs.
are annihilation (creation) operators of the single level QDs. 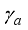 and
and 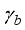 are the Majorana operators associated with the two MBSs at the ends of the nano-wire.
are the Majorana operators associated with the two MBSs at the ends of the nano-wire. 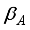 and
and 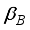 are respectively the coupling amplitudes between Majorana end states of QD A1 and QD B1. In our studies we will consider symmetric and asymmetric coupling between the Majorana end modes and the dots. Following the transformations as reported in
are respectively the coupling amplitudes between Majorana end states of QD A1 and QD B1. In our studies we will consider symmetric and asymmetric coupling between the Majorana end modes and the dots. Following the transformations as reported in 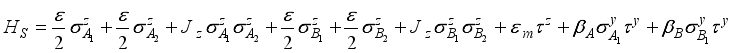 (3)
(3) 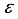 is the single particle energy of each dot (qubit) and
is the single particle energy of each dot (qubit) and 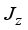 the exchange coupling along the z-axis (Ising model) and describes the interaction between the qubits of the individual sub-systems A and B.
the exchange coupling along the z-axis (Ising model) and describes the interaction between the qubits of the individual sub-systems A and B. 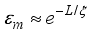 is the strength of the two Majorana interaction that damps exponentially with the length of the nano-wire L,
is the strength of the two Majorana interaction that damps exponentially with the length of the nano-wire L, 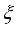 is the superconducting coherent length.
is the superconducting coherent length. 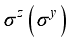 and
and 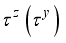 represents the Pauli spin operators for the dots qubits and Majorana qubit respectively. In the fermionic representation of the systems Hamiltonian equation (2), we use the state basis,
represents the Pauli spin operators for the dots qubits and Majorana qubit respectively. In the fermionic representation of the systems Hamiltonian equation (2), we use the state basis, 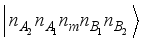 describing the possible spin configuration of sub-system A, MBSs and sub-system B, where
describing the possible spin configuration of sub-system A, MBSs and sub-system B, where 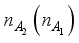 for sub-system A,
for sub-system A, 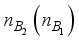 for sub-system B and
for sub-system B and 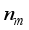 MBSs, represents their respective spin ‘up’ or ‘down’ sates. Synonymous to the subspace with odd charge parity, we consider the following subspaces with spin configurations:
MBSs, represents their respective spin ‘up’ or ‘down’ sates. Synonymous to the subspace with odd charge parity, we consider the following subspaces with spin configurations: 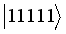 ,
, 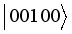 ,
, 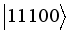 ,
, 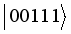 ,
, 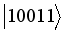 ,
, 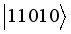 ,
, 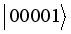 ,
, 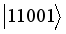 ,
, 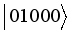 ,
, 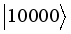 ,
, 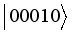 . The Hamiltonians:
. The Hamiltonians: 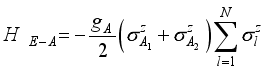 (4)
(4) 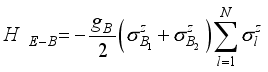 (5)
(5) 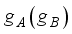 the strength of their respective interactions.
the strength of their respective interactions. 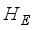 represents that of the spin environment which we consider the same for the two separate pairs of qubits, is described by the one-dimensional XY model written in the unit where
represents that of the spin environment which we consider the same for the two separate pairs of qubits, is described by the one-dimensional XY model written in the unit where 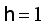 , is given by
, is given by 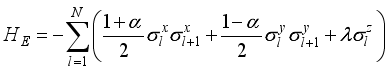 (6)
(6) 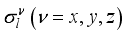 describe the spin chain of the environment. The parameter
describe the spin chain of the environment. The parameter 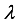 characterizes the intensity of the transverse magnetic field, and
characterizes the intensity of the transverse magnetic field, and 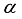 measures the anisotropy in the in-plane interaction. The XY model described by equation (6) encompasses other two spin model; the Ising spin chain with
measures the anisotropy in the in-plane interaction. The XY model described by equation (6) encompasses other two spin model; the Ising spin chain with 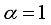 and the XX spin chain with
and the XX spin chain with 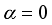 . These different models shall be subject to our investigation. Following the result of the treatment in
. These different models shall be subject to our investigation. Following the result of the treatment in 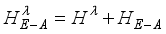 (7)
(7) 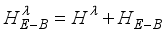 (8)
(8) 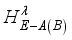 of the two qubits of sub-system A(B) dressed with the environment due to interaction is given by
of the two qubits of sub-system A(B) dressed with the environment due to interaction is given by 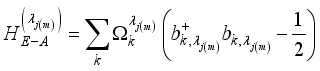 (9)
(9) 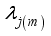 correspond to the dressed eigen value due to interactions of sub-systems A(B) with their respective spin chain enviroment.
correspond to the dressed eigen value due to interactions of sub-systems A(B) with their respective spin chain enviroment. 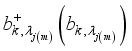 are the Bogoliubov-transformed annihilation (creation) fermion operators arising from the interactions between the two qubits and the environment, defined as
are the Bogoliubov-transformed annihilation (creation) fermion operators arising from the interactions between the two qubits and the environment, defined as 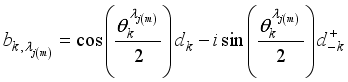 (10)
(10) 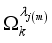 is given by
is given by 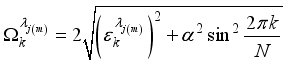 , with
, with 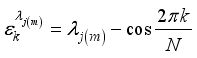 .
. 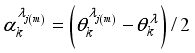 with angles
with angles 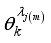 satisfying,
satisfying, 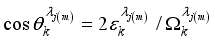 . We note that the energy spectrum
. We note that the energy spectrum 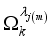 carries information about all the possible excitations in the spin chain. Interaction between the spin chain and qubits induces overlap between these excitations and thus quantum fluctuations.
carries information about all the possible excitations in the spin chain. Interaction between the spin chain and qubits induces overlap between these excitations and thus quantum fluctuations. 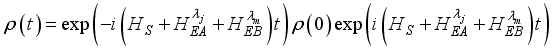 (11)
(11) 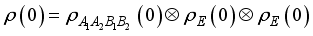 .
. 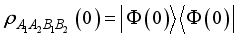 is the density matrix of sub-system A, MBS and sub-system B in the initial state.
is the density matrix of sub-system A, MBS and sub-system B in the initial state. 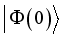 is the initial prepared state of the system Hamiltonian assumed to be in the general form:
is the initial prepared state of the system Hamiltonian assumed to be in the general form: 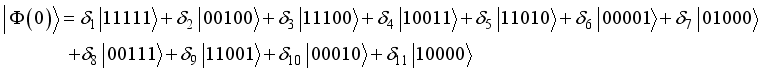 (12)
(12) 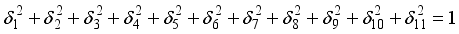 (13)
(13) 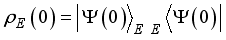 describes the density matrix of the spin chain in the initial state
describes the density matrix of the spin chain in the initial state 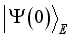 . Tracing the environmental degrees of freedom leads to the following equation of the time evolving density matrix:
. Tracing the environmental degrees of freedom leads to the following equation of the time evolving density matrix: 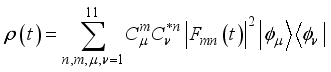 (14)
(14) 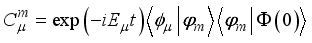 and
and 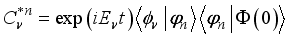 .
. 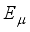 and
and 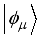 are respectively the eigen value and eigen state of the system Hamiltonian equation (3). The absolute value of the decoherence factor
are respectively the eigen value and eigen state of the system Hamiltonian equation (3). The absolute value of the decoherence factor 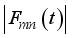 written in the form as given in
written in the form as given in 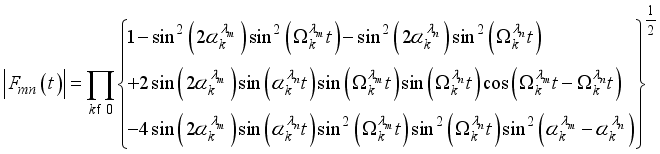 (15)
(15) 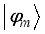 written in the basis:
written in the basis: 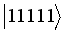 ,
, 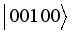 ,
, 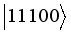 ,
, 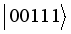 ,
, 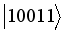 ,
, 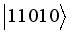 ,
, 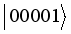 ,
, 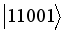 ,
, 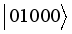 ,
, 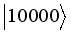 ,
, 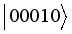 are those of the interaction Hamiltonians as discussed earlier of sub-system A and B interacting with their spin environment. The corresponding eigen values are:
are those of the interaction Hamiltonians as discussed earlier of sub-system A and B interacting with their spin environment. The corresponding eigen values are: 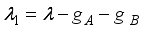 ,
, 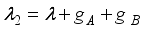 ,,
,, 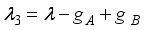
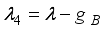 ,
, 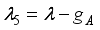 ,
, 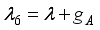 ,
, 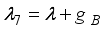 ,
, 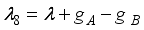 ,
, 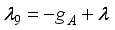 ,
, 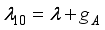 ,
, 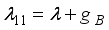
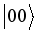 ,
, 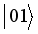 ,
, 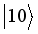 ,
, 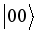 is given as
is given as 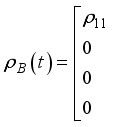
 (16)
(16) 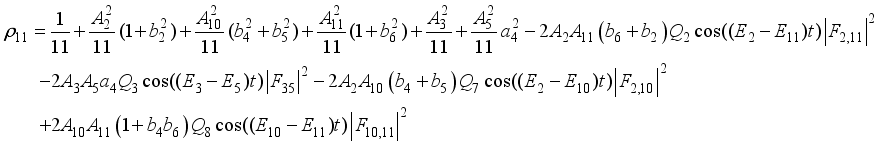
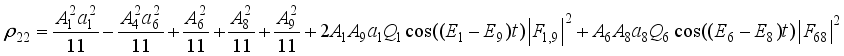
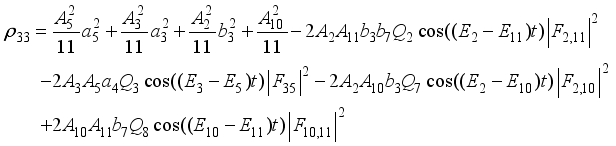
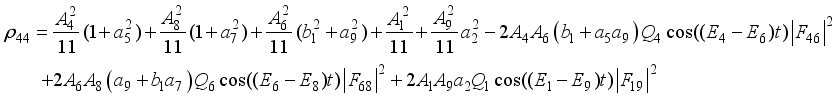
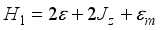 ,
, 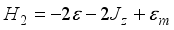 ,
, 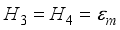 ,
, 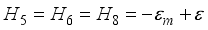 ,
, 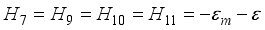 ,
, 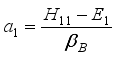 ,
, 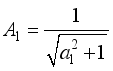 ,
, 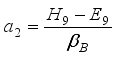 ,
, 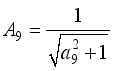 ,
, 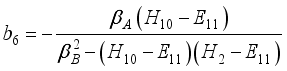 ,
, 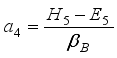 ,
, 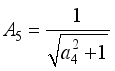 ,
, 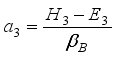 ,
, 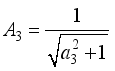 ,
, 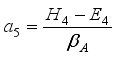 ,
, 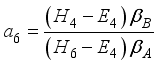
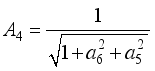 ,
, 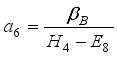 ,
, 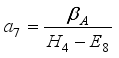 ,
, 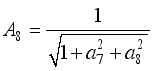 ,
, 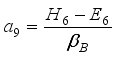 ,
, 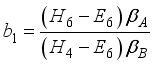 ,
, 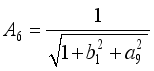 ,
, 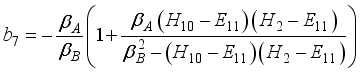 ,
, 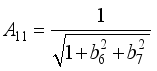 ,
, 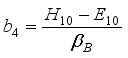 ,
, 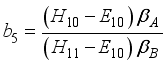 ,
, 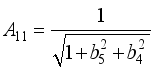 ,
, 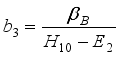 ,
, 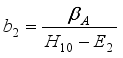 ,
, 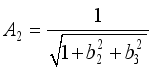 ,
, 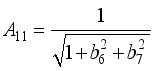 ,
, 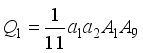 ,
, 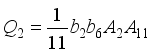 ,
, 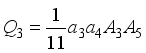 ,
, 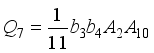 ,
, 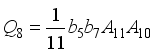 .
. 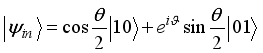 and
and 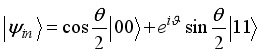 with
with 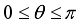 and
and 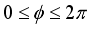 .
. 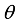 represent the amplitude and
represent the amplitude and 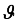 the phase of the input state. The density matrix related to the input state is
the phase of the input state. The density matrix related to the input state is 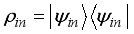 . The output state can be obtained by applying joint measurements and local unitary transformations on the input state
. The output state can be obtained by applying joint measurements and local unitary transformations on the input state 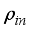 . Following the teleportation protocol proposed by Lee and Kim the output state of the two qubit teleportation can be written as
. Following the teleportation protocol proposed by Lee and Kim the output state of the two qubit teleportation can be written as 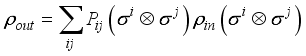 , where
, where 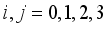 and
and 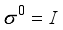 is the identity matrix,
is the identity matrix, 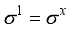 ,
, 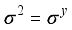 ,
, 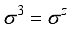 are the Pauli matrices. The probabilities
are the Pauli matrices. The probabilities 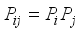 satisfy the condition
satisfy the condition 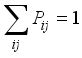 , with
, with 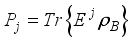 and
and 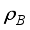 being the reduced density matrix of the channel corresponding to system B. The projective measurements
being the reduced density matrix of the channel corresponding to system B. The projective measurements 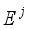 are defined from the four maximally entangle Bell states as
are defined from the four maximally entangle Bell states as 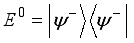 ,
, 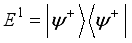 ,
, 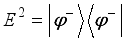 ,
, 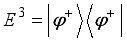 , where
, where 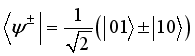 and
and 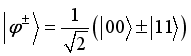 .
. 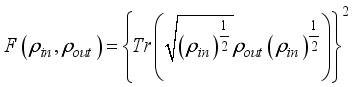 . To efficiently measure the quality of the protocol, we calculate the average fidelity between the input and output states by averaging over all possible input states. Under the influence of the environment and channel parameters, the maximally entangled component can vary with time. Therefore, the best quality of the teleportation can be obtained by the optimal estimation of the projective measurements. Thus the average fidelity will be a function of time. The average fidelity is defined from the fidelity as
. To efficiently measure the quality of the protocol, we calculate the average fidelity between the input and output states by averaging over all possible input states. Under the influence of the environment and channel parameters, the maximally entangled component can vary with time. Therefore, the best quality of the teleportation can be obtained by the optimal estimation of the projective measurements. Thus the average fidelity will be a function of time. The average fidelity is defined from the fidelity as 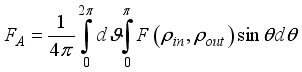 . From straight evaluation we obtain the fidelity and average fidelity for the input state
. From straight evaluation we obtain the fidelity and average fidelity for the input state 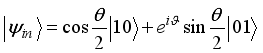 respectively as:
respectively as: 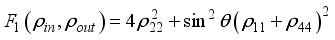 (17)
(17) 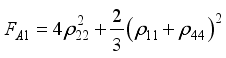 .(18)
.(18) 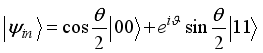 we have the fidelity and average fidelity respectively as:
we have the fidelity and average fidelity respectively as: 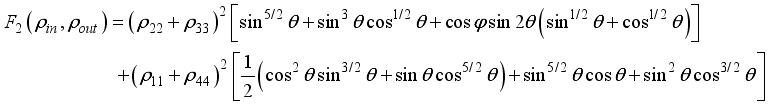 (19)
(19) 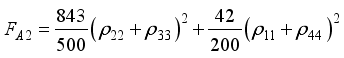 (20)
(20) 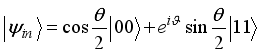 and
and 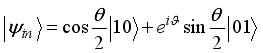 with corresponding average fidelities
with corresponding average fidelities 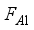 and
and 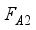 given in equations (18) and (20) respectively, in Figure 2. The same trend in the dynamics is observed in both cases however with enhancement when the entangled input state,
given in equations (18) and (20) respectively, in Figure 2. The same trend in the dynamics is observed in both cases however with enhancement when the entangled input state, 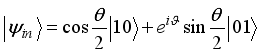 is used. Figure 2(b) is the scenario when the values of the coupling between the spin chain and the two qubits sub-systems are interchanged.
is used. Figure 2(b) is the scenario when the values of the coupling between the spin chain and the two qubits sub-systems are interchanged. 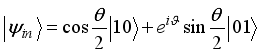 with average fidelity given by
with average fidelity given by 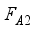 .
. 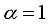 , showing enhancement in the dynamics of teleportation after a short period of time. This scenario has already been reported in
, showing enhancement in the dynamics of teleportation after a short period of time. This scenario has already been reported in 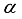 . Large values of the anisotropy parameter strengthens the interactions between the atomic spin environment and coherent excitations having less decoherence effect prevails in the spin environment, as compared to small values of the anisotropy parameter that makes the spin environment prone to quantum fluctuations and increasing decoherence effects on the dynamics of the teleported states.
. Large values of the anisotropy parameter strengthens the interactions between the atomic spin environment and coherent excitations having less decoherence effect prevails in the spin environment, as compared to small values of the anisotropy parameter that makes the spin environment prone to quantum fluctuations and increasing decoherence effects on the dynamics of the teleported states. 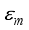 . We see that as the values of the coupling between the MBSs state increases, the average fidelity of teleportation decreases. Large values of
. We see that as the values of the coupling between the MBSs state increases, the average fidelity of teleportation decreases. Large values of 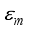 corresponds to very small wire length that lead to overlap between the Majorana end modes which may intend lifting of the topological phase that harbour’s the Majorana bound state. In the opposite scenario, small values imply long wire length and enhancement in the teleportation state. This owes explanation from non-locality of the MBSs. We recollect that in
corresponds to very small wire length that lead to overlap between the Majorana end modes which may intend lifting of the topological phase that harbour’s the Majorana bound state. In the opposite scenario, small values imply long wire length and enhancement in the teleportation state. This owes explanation from non-locality of the MBSs. We recollect that in 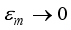 (very long wire length), a remarkable teleportation feature known as superluminal holds in electron transport.
(very long wire length), a remarkable teleportation feature known as superluminal holds in electron transport. MBSs | Majorana Bound States |
QD | Quantum Dot |
SMW | Single Majorana Wire |
DMWs | Double Majorana Wires |
| [1] | A. E. Ngwa, F. C. Lukong, M. Ateuafack, F. C. Georges and N. J. Carsimir, “Entanglement teleportation between distinct decohered qubits mediated via single and double Majorana wire(s),” Phys. Scr. 95 035803 (2020), |
| [2] | S. Bose, “Quantum computation through un-modulated spin chain,” Phys. Rev. Lett. 91 207901-4 (2003), |
| [3] | V. Subrahmanyam, “Entanglement dynamics and quantum state transport in spin chain,” Phys. Rev. A 69 034304-7 (2004), |
| [4] | A. Kay, “Unifying quantum state transfer and state amplification,” Phys. Rev. Lett. 98 010501-4 (2007), |
| [5] | K. Eckert, O. Romero-Isart, and A. Sanpera, “Efficient quantum state transfer in spin chain via adiabatic passage,” New J. Phys. 9 155-73 (2007), |
| [6] | A. Kay, “Tailoring spin chain dynamics for fractional revivals,” Quantum 1, 24 (2017), |
| [7] | J. G. Apollaro, M. G. Guilherme, S. Lorenzo, A. Ferraro, and S. Paganelli, “Spin chains for two-qubit teleportation,” Phys. Rev A. 100.052308 (2019), |
| [8] | J. G. Appolaro, S. Lorenzo, A. Sindona, S. Paganelli, GL. J. iorgi, F. Plastina, “Many qubits quantum state transfer via spin chains,” Physica script A, 165, 014036 (2015), |
| [9] | V. Harshit, C. Levan, B. Jamal, M. K. Sunil, “Quantum teleportation by utilizing helical spin chains for sharing entanglement,” Quantum Inf Process 20, 54 (2021), |
| [10] | A. Slaoui, E. A. Kirdi, A. R. Laamara, M. Alabdulhafith, A. S. Chelloug and Abd El-Latif, “Cyclic quantum teleportation of two-qubit entangled states by using six-qubit cluster state and six-qubit entangled state,” Sci. Rep. 14: 15856 (2024), |
| [11] | J. Li, T. Y. Ting, Q. H. Lin and Q. J. You, “Probing the nonlocality of Majorana fermions via quantum correlations,” Sci. Rep. 4 4930 (2014), |
| [12] | A. Y. Kitaev, “Fault-tolerant quantum computation by anyons,” Ann. Phys., NY 303 2-30 (2003), |
| [13] | D. S. Sarm, M. Freedman and C. Nayak, “Topological quantum computation,” Phys. Today S-0031-9228-06070-020-7 (2006), |
| [14] | C. Nayak, S. H. Steven, A. Stern, F. Michael, and D. S. Sankar, “Non-Abelian anyons and topological quantum computation,” Rev. Mod. Phys. 80 1083 (2008), |
| [15] | T. E. O’Brien, P. Rozek and A. R. Akhmerov “Majorana-Based fermionic Quantum computation,” Phys. Rev. Lett. 120, 220504 (2018), |
| [16] | G. Moore and N. Read, “Paired states of fermions in two dimensions with breaking of parity and time reversal symmetries and the fractional quantum Hall effect,” Phys. Rev. B 61 10267 (2000), |
| [17] | A. Y. Kitaev, “Unpaired Majorana fermions in quantum wires,” Phys.-Usp. 44 131-6 (2001), |
| [18] | L. Fu and C. Kane, “Superconducting proximity effect and Majorana fermions at the surface of a topological insulator,” Phys. Rev. Lett. 100 096407 (2008), |
| [19] | Y. Oreg, G. Refael and F. von Oppen F, “Helical liquids and Majorana bound states in quantum wires,” Phys. Rev. Lett. 105 177002 (2010), |
| [20] | L. Xin-Qi and X. Lutin, “Revisite the non-locality of Majorana Zero mode and teleportation: Bogoluibov-de Gennes equation based treatment,” Phys. Rev. B 101, 205401 (2020), |
| [21] | S. L. Ricco, A. F. Dessotti, A. I. Shelykh, M. S. Figueira and A. C. Seridonio, “Tuning of heat and charge transport by Majorana fermions,” Sci. Rep. 8 2790 (2018), |
| [22] | P. Wang, Y. Cao, M. Gong, S. S. Li and L. Xin-Qi L, “Cross-correlations mediated by Majorana bound states,” Euro phys. Lett. 103 57016 (2013), |
| [23] | P. Wang, Y. Cao, M. Gong, S. S. Li and L. Xin-Qi, “Demonstrating Nonlocality Induced Teleportation Through Majorana Bound States in a Semiconductor Nanowire,” J. Phys. Lett. A. 2014.01.039 (2014), |
| [24] | P. Stephan, Z. Alex, S. Pasquale and E. Reinhold, “Majorana Entanglement Bridge,” Phys. Rev. B 91, 214507 (2015), |
| [25] | E. Ferraro, D. M. Michielis, G. Mazzeo, M. Fanciulli and E. Prati “Effective Hamiltonian for the hybrid double quantum dot qubit,” Quantum Inf. Process 13, 1155-1173 (2014), |
| [26] | G. Z. Yuan, P. Zhang, and S. S. Li, “Disentanglement of two qubits coupled to an XY spain chain: Rolle of quantum phase transition,” Phys. Rev. A 76, 042118 (2007), |
| [27] | J. Nie, C. Wang Lin and Y. Xue-Xi, “Disentanglement of two qubits Coupled to an XY spin chain at finite Temperature,” Commun. Theor. Phys. 51, pp. 815-819 (2009), |
| [28] | W. W. Cheng, and M. J. Liu, “Decoherence from spin environment: role of the Dzyaloshinsky-Moriya interaction,” Phys. Rev. A 79 052320 (2009), |
APA Style
Afuoti, N. E., Fai, L. C., Pierre, N. J., Ngana, J. C., Mathurin, A., et al. (2025). Average Fidelity of Two Qubits Entanglement Teleportation Mediated Via a Single Majorana Wire. American Journal of Modern Physics, 14(5), 222-233. https://doi.org/10.11648/j.ajmp.20251405.12
ACS Style
Afuoti, N. E.; Fai, L. C.; Pierre, N. J.; Ngana, J. C.; Mathurin, A., et al. Average Fidelity of Two Qubits Entanglement Teleportation Mediated Via a Single Majorana Wire. Am. J. Mod. Phys. 2025, 14(5), 222-233. doi: 10.11648/j.ajmp.20251405.12
@article{10.11648/j.ajmp.20251405.12,
author = {Ngwa Engelbert Afuoti and Lukong Cornelius Fai and Nguenang Jean Pierre and Jules Carsimir Ngana and Ateuafack Mathurin and Georges Collince Fouokeng},
title = {Average Fidelity of Two Qubits Entanglement Teleportation Mediated Via a Single Majorana Wire
},
journal = {American Journal of Modern Physics},
volume = {14},
number = {5},
pages = {222-233},
doi = {10.11648/j.ajmp.20251405.12},
url = {https://doi.org/10.11648/j.ajmp.20251405.12},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.ajmp.20251405.12},
abstract = {We revisit the teleportation of two qubits entanglement using a single channel made of a single Majorana wire connecting two pairs of qubits each at the sending and receiving ends of the wire. The scheme is different from that use in our early work (Phys. Scr. 95 035803 (2020)) where the two qubit teleportation required two copies of the Majorana wires setup as required to implement the Lee and Kim teleportation scheme. The two pairs of qubit interact via the exchange coupling. It is in this setting that we investigate the role of the exchange coupling, the channel parameters, the spin chain parameters on the average fidelity of entanglement teleportation. We equally consider the fact that the geographically located two pairs of qubits interact differently with their respective spin chain environment. The dynamics of the average fidelity is shown to be enhanced when using a set-up with symmetric coupling between qubits and Majorana wire at both ends as compared to when using asymmetric coupling. Small values of the coupling between the qubits and spin environments should however be used. Large values of the exchange coupling between qubits in the two sub-systems should be used to have high fidelity of the teleported state. The dynamics of the average fidelity of entanglement teleportation is seen to depend on the size of the spin environment as compared to the teleportation protocol used in our earlier work where the dynamics is mildly sensitive to the size of the spin environment. Increasing the strength of the transverse magnetic field and large values of the anisotropy degree enhances the average fidelity of entanglement teleportation. The same observation is seen when considering the same values of the coupling between the two qubits sub-systems at the opposite ends of the Majorana wire and their respective spin environment. The dynamics of the system is however seen to observe almost a similar trend as that of the above cited work for the single Majorana wire setup.
},
year = {2025}
}
TY - JOUR T1 - Average Fidelity of Two Qubits Entanglement Teleportation Mediated Via a Single Majorana Wire AU - Ngwa Engelbert Afuoti AU - Lukong Cornelius Fai AU - Nguenang Jean Pierre AU - Jules Carsimir Ngana AU - Ateuafack Mathurin AU - Georges Collince Fouokeng Y1 - 2025/10/27 PY - 2025 N1 - https://doi.org/10.11648/j.ajmp.20251405.12 DO - 10.11648/j.ajmp.20251405.12 T2 - American Journal of Modern Physics JF - American Journal of Modern Physics JO - American Journal of Modern Physics SP - 222 EP - 233 PB - Science Publishing Group SN - 2326-8891 UR - https://doi.org/10.11648/j.ajmp.20251405.12 AB - We revisit the teleportation of two qubits entanglement using a single channel made of a single Majorana wire connecting two pairs of qubits each at the sending and receiving ends of the wire. The scheme is different from that use in our early work (Phys. Scr. 95 035803 (2020)) where the two qubit teleportation required two copies of the Majorana wires setup as required to implement the Lee and Kim teleportation scheme. The two pairs of qubit interact via the exchange coupling. It is in this setting that we investigate the role of the exchange coupling, the channel parameters, the spin chain parameters on the average fidelity of entanglement teleportation. We equally consider the fact that the geographically located two pairs of qubits interact differently with their respective spin chain environment. The dynamics of the average fidelity is shown to be enhanced when using a set-up with symmetric coupling between qubits and Majorana wire at both ends as compared to when using asymmetric coupling. Small values of the coupling between the qubits and spin environments should however be used. Large values of the exchange coupling between qubits in the two sub-systems should be used to have high fidelity of the teleported state. The dynamics of the average fidelity of entanglement teleportation is seen to depend on the size of the spin environment as compared to the teleportation protocol used in our earlier work where the dynamics is mildly sensitive to the size of the spin environment. Increasing the strength of the transverse magnetic field and large values of the anisotropy degree enhances the average fidelity of entanglement teleportation. The same observation is seen when considering the same values of the coupling between the two qubits sub-systems at the opposite ends of the Majorana wire and their respective spin environment. The dynamics of the system is however seen to observe almost a similar trend as that of the above cited work for the single Majorana wire setup. VL - 14 IS - 5 ER -